Jensen’s inequality
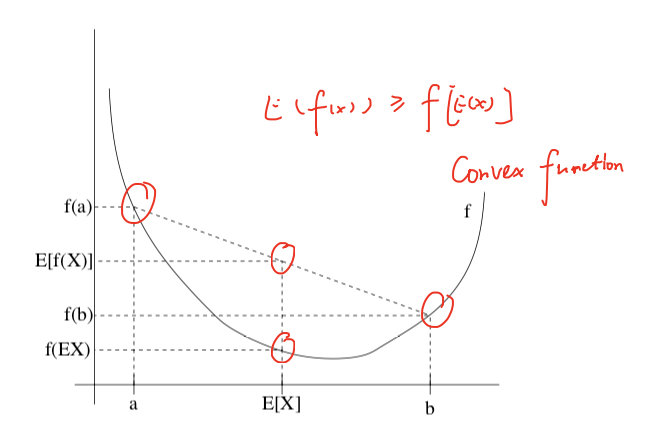
定理:若f是凸函数,X是随机变量,我们有:E[f(X)]≥f(EX)
- 若f是严格凸函数,也就是f′′>0恒成立,同时X=E[X](也就是X是常数的概率为1),则等号成立。
- 若f是凹函数,则该定理也成立,只不过将大于等于换成小于等于。
忽略证明,该定理并不直观,可以用一个简单的例子帮助记忆:
收敛性证明
我们想用模型拟合数据,也就是求似然函数:
ℓ(θ)=i=1∑mlogp(x;θ)=i=1∑mlogz∑p(x,z;θ)
其中,z是隐变量。如果z已知,那么直接用MLE求解即可,如果未知,则需要用EM算法迭代求解。
EM算法分为两步:
- E step:每次得到似然函数ℓ的一个下界。
- M step:对该下界进行优化。
我们首先可以假设Q是z的分布,也就是满足:∑zQi(z)=1,Qi(z)≥1
我们的目标是最大化似然函数, 因此可以得到:
i∑logp(x(i);θ)=i∑logz(i)∑p(x(i),z(i);θ)=i∑logz(i)∑Qi(z(i))Qi(z(i))p(x(i),z(i);θ)≥i∑z(i)∑Qi(z(i))logQi(z(i))p(x(i),z(i);θ)
这里用到了..期望就是概率..的思想。我们将Q函数看成是在随机变量Qi(z(i))p(x(i),z(i);θ)上的概率分布,将函数f看成是log function。因此,第二个等式可以看作是f(EX)。而由于f函数是凹函数,因此根据Jensen’s inequality,可以得到不等式三。
这样,对于任意的分布Q,我们给出了似然函数的下界。因此,我们如何选择一个合适的Q呢(最好能取到等号)?
我们如果对当前的θ有一个估计值,那么很自然的思想就是用这个估计值来得到不等式的下界。根据之前Jensen’s inequality不等式的分析,如果我们的随机变量是一个常量,那么等式一定成立,即:
Qi(z(i))p(x(i),z(i);θ)=c
因此,我们只需要Qi(z(i))∝p(x(i),z(i);θ)即可。同时,由于∑zQi(z(i))=1的条件需要满足,因此构造一个Q函数为:
Qi(z(i))=∑zp(x(i),z;θ)p(x(i),z(i);θ)=p(x(i);θ)p(x(i),z(i);θ)=p(z(i)∣x(i);θ)
实际上,这个Q函数就是我们熟悉的在给定θ下的后验分布。
如何证明收敛性呢?也就是需要证明ℓ(θ(t))≤ℓ(θ(t+1))始终成立。
由于我们选择的Q函数能使得等式成立,因此在第t次迭代时,有:
ℓ(θ(t))=i∑z(i)∑Qi(t)(z(i))logQi(t)(z(i))p(x(i),z(i);θ(t))
在第t+1次时,我们的θ(t+1)是最大化右边的式子的来的,因此:
ℓ(θ(t+1))≥i∑z(i)∑Qi(t)(z(i))logQi(t)(z(i))p(x(i),z(i);θ(t+1))≥i∑z(i)∑Qi(t)(z(i))logQi(t)(z(i))p(x(i),z(i);θ(t))=ℓ(θ(t))
其中,第一个不等式是根据Jensen’s inequality,第二个不等式是根据最大化θ的性质来的。
如果我们定义:
J(Q,θ)=i∑z(i)∑Qi(z(i))logQi(z(i))p(x(i),z(i);θ)
那么,EM算法也可以看作是在J上进行coordinate ascent:
- E step 时,固定θ,根据Q最大化J
- 实际上是通过Jensen’s inequality的性质,定义Q函数为后验概率满足等式)
- M step 时,固定Q,根据θ最大化J
GMM revisited
GMM的思想不再阐述,这里主要进行推导closed form。
E step
E step相对容易一些,我们对于当前步估计的所有参数值,计算z的后验分布(这样能保证在当前参数下等式成立,也就是tight bound):
wj(i)=Qi(z(i)=j)=P(z(i)=j∣x(i);ϕ,μ,Σ)
M step
根据上一步得到的z的分布,我们最大化ℓ的下界:
i=1∑mz(i)∑Qi(z(i))logQi(z(i))p(x(i),z(i);ϕ,μ,Σ)=i=1∑mj=1∑kQi(z(i)=j)logQi(z(i)=j)p(x(i)∣z(i)=j;μ,Σ)p(z(i)=j;ϕ)=i=1∑mj=1∑kwj(i)logwj(i)(2π)n/2∣Σj∣1/21exp(−21(x(i)−μj)TΣj−1(x(i)−μj))⋅ϕj
我们只需要分别对三个参数进行求导,即可得到:
μl:=∑i=1mwl(i)∑i=1mwl(i)x(i)
ϕj:=m1i=1∑mwj(i)
Σj:=∑i=1mwj(i)∑i=1mwj(i)(x(i)−μj)(x(i)−μj)T
这也就是我们上一个博客给出的EM算法的迭代过程。
